
В последующие века, после того как древние греки первыми их вывели, парадоксы процветали во всех слоях общества, радуя и приводя в бешенство миллионы людей. Некоторые из них представляют проблемы с нелогичными ответами, остальные — неразрешимые проблемы. Мы выбрали десятку самых любопытных и малоизвестных.
Демон Максвелла
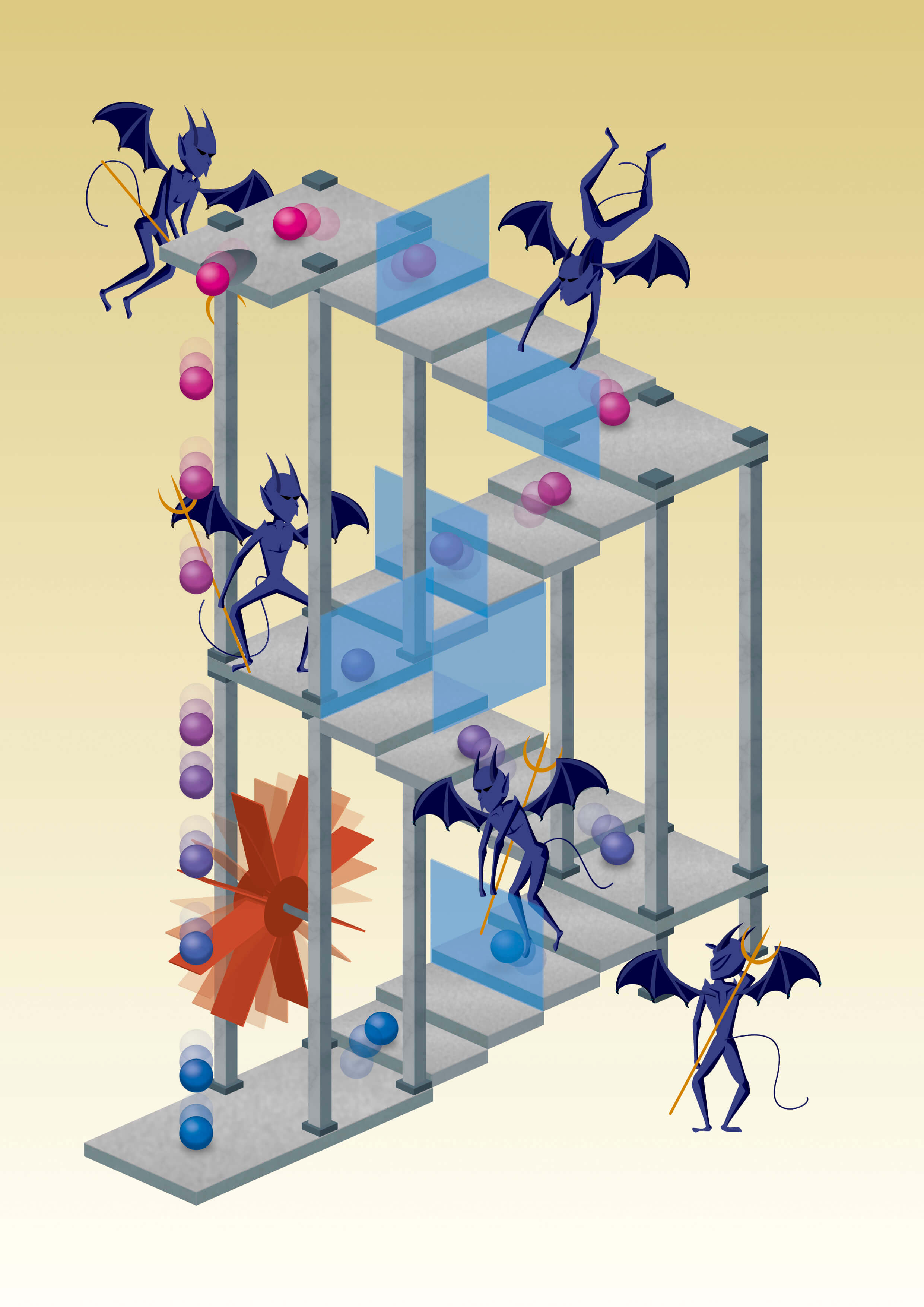
Названный в честь шотландского физика 19 века, первым предложившим эту идею, «демон Максвелла» — это мысленный эксперимент, в котором Джеймс Клерк Максвелл пытался нарушить второй закон термодинамики. Законы Ньютона остаются нерушимыми, поэтому сам факт возможности их нарушения привел к парадоксу.
Есть коробка, заполненная газом неопределенной температуры. В середине коробки есть стенка. Некий демон открывает отверстие в стене, позволяя только быстрым (в среднем) молекулам проникнуть в левую часть коробки. Таким образом, демон создает две отдельные зоны: горячую и холодную. Разделение температур позволяет, в свою очередь, генерировать энергию, позволяя потоку молекул перетекать от горячей к холодной областям через тепловой двигатель. На первый взгляд, такая система должна нарушить второй закон Ньютона, который утверждает, что энтропию изолированной системы невозможно изменить.
Однако второй закон говорит и то, что демон не сможет делать это без ежеминутной потери своей энергии. Такое опровержение было впервые предложено венгерским физиком Лео Сцилардом. Смысл этого аргумента в том, что демон будет генерировать энтропию простым измерением того, какие молекулы движутся быстрее среднего. Кроме того, движение дверей и движение демона тоже будет генерировать энтропию.
Лампа Томсона

Джеймс Томсон был британским философом, жившим в 20 веке. Его наиболее заметным вкладом стал парадокс, известный как «лампа Томсона», головоломка, связанная с таким явлением, как сверхзадачи. (Сверхзадачи — это счетные бесконечные последовательности, которые происходят в определенном порядке в конечное время).
Проблема такова. Есть лампа с кнопкой. Нажатие кнопки включает и выключает свет. Если каждое последующее нажатие кнопки будет занимать в два раза меньше времени, чем предыдущее, будет ли свет включен или выключен спустя заданный промежуток времени?
Благодаря природе бесконечности, невозможно узнать, будет ли свет включен или выключен, поскольку последнего нажатия на кнопку просто не будет. За любое время, хоть за две минуты, хоть за десять, на выключатель придется нажать бесконечное число раз. Сверхзадачи были впервые предложены Зеноном Элейским, а Томсон довел эту задачу до парадокса. Некоторые философы вроде Пола Бенасеррафа все еще утверждают, что машины вроде лампы Томсона как минимум логически возможны.
Проблема двух конвертов

Менее известный двоюродный брат «парадокса Монти Холла» — «проблема двух конвертов» — объясняется следующим образом. Человек показывает вам два конверта. Он говорит, что в одном лежит определенная сумма долларов, а в другом — в два раза больше. Вам нужно выбрать конверт и проверить содержимое. Затем вы можете выбрать: оставить себе конверт или взять другой. Какой даст вам больше денег? При условии, что вы не знаете, сколько конкретно денег лежит в вашем или другом конверте.
Изначально ваш шанс взять конверт с большим количеством денег составляет 50/50, или 1 к 2. Самая распространенная ошибка, которую допускают при вычислении лучшего варианта, заключается в следующей формуле, где Y — ценность конверта в вашей руке: 1/2(2Y) + 1/2(Y/2) = 1,25Y. Проблема этого решения в том, что вам нужно сделать бесконечное число выборов, поскольку именно так вы будете получать больше денег. В этом и парадокс. Было выдвинуто много решений, но ни один из них не был принят широко.
Парадокс мальчика или девочки

Допустим, в семье есть двое детей. Учитывая то, что вероятность наличия мальчика равна 1/2, каковы шансы того, что другой ребенок тоже мальчик? Интуиция подсказывает, что опять 1/2, но это не так. Правильный ответ — 1/3.
Есть четыре варианта для семьи с двумя детьми: старший брат с младшей сестрой (МД), старший брат с младшим братом (ББ), старшая сестра с младшим братом (ДМ) или старшая сестра с младшей сестрой (ДД). Мы знаем, что вариант ДД невозможен, потому что в семье уже есть один мальчик. Таким образом, возможны лишь варианты МД, ББ и ДМ. Вероятность 1/3. Можно еще поспорить о близнецах, но технически они рождаются не одновременно.
Дилемма крокодила

Разновидность парадокса лжеца, которую популяризовал древнегреческий философ Евболид. «Дилемма крокодила» сложилась следующим образом. Крокодил украл ребенка у его родителя и затем говорит родителю, что вернет ребенка, если родитель правильно угадает, вернет ли крокодил ребенка или нет. Если родитель скажет «ты вернешь мое дитя», все в порядке и ребенок вернется. Но если родитель скажет «ты не вернешь моего ребенка», возникает парадокс.
Парадокс в том, что если крокодил вернет ребенка, он нарушит свое слово, так как родитель не угадал. Однако если крокодил не вернет ребенка, он тоже нарушит свое слово, так как родитель угадал. Видимо, ребенку уготовано остаться в пасти крокодила, поскольку пара никогда не договорится. Псевдорешение этого парадокса — тайно уведомить третью сторону в истинном намерении крокодила. Тогда крокодил сдержит свое обещание вне зависимости от ответа.
Парадокс слабого молодого Солнца

Этот астрофизический парадокс возник, когда мы осознали, что наше Солнце почти на 40% ярче, чем было почти четыре миллиарда лет назад. Однако, если это действительно было так, Земля должна была получать намного меньше тепла в прошлом, а значит поверхность планеты была бы сплошь заморожена. Впервые поднятый ученым Карлом Саганом в 1972 году, парадокс слабого молодого Солнца поставил в тупик все научное сообщество, поскольку геологические свидетельства показывают, что нашу планету покрывали океаны почти всегда.
В качестве возможного решения были предложены парниковые газы. Но их уровень должен был быть в сотни или тысячи раз выше, чем сейчас. Плюс есть масса свидетельств того, что такого не было. Возможно, свою роль сыграла некая «планетарная эволюция». Согласно этой теории, условия Земли (вроде химического состава атмосферы) менялись по мере развития жизни.
Парадокс Гемпеля

Известный также как «парадокс воронов», парадокс Гемпеля — это вопрос о природе доказательств. Он начинается с утверждения «все вороны черные» и логически контрапозитивного заявления «все не черные вещи — не вороны». Затем философ утверждает, что всякий раз, когда видно ворона — а все вороны черные — первое утверждение подтверждается. Кроме того, всякий раз, когда видно не черный объект вроде зеленого яблока, подтверждается второе утверждение.
Парадокс возникает потому, что каждое зеленое яблоко также предоставляет доказательства того, что все вороны черные, так как две гипотезы логически эквивалентны. Наиболее широко распространенным «решением» проблемы будет договоренность о том, что каждое зеленое яблоко (или белый лебедь) приводит доказательство того, что вороны черные, но с оговоркой, что количество доказательств будет настолько малым, что станет несущественным.
Парадокс парикмахерской

В июле 1894 года в Mind (британский научный журнал) Льюис Кэрролл, автор «Алисы в Стране Чудес», предложил парадокс, известный как «парадокс парикмахерской». Выглядит он так. Дядя Джо и дядя Джим шли к парикмахерской, обсуждая трех парикмахеров — Карра, Аллена и Брауна. Дядя Джим хотел, чтобы его стриг Карр, но не был уверен, что Карр работает. Один из трех парикмахеров работал, потому что парикмахерская была открыта. Они также знали, что Аллен никогда не уходит из парикмахерской без Брауна.
Дядя Джо утверждал, что может логически доказать, что Карр работает, потому что он должен работать всегда, поскольку Браун не будет работать без Аллена. Однако парадокс в том, что Аллен мог быть внутри, а Браун мог быть дома. Дядя Джо утверждал, что это приводит к двум противоречивым заявлениям, а значит Карр должен быть внутри. Современные логики доказали, что технически это не парадокс. Единственное, что имеет значение — если Карр не работает, значит, работает Аллен, а кому какое дело до Брауна?
Парадокс Галилея

Более известный своими работами в астрономии, Галилей также пробовал себя и в математике и вывел парадокс о бесконечности и квадратах натуральных чисел. Он первым заявил, что есть некоторые положительные целые числа, которые являются квадратами, и некоторые, которые не являются. Таким образом, он предположил, что сумма этих двух групп должна быть больше суммы только группы квадратов. Выглядит здраво.
Тем не менее парадокс возникает потому, что у любого натурального числа есть квадрат, а у каждого квадрата — натуральное положительное число, которое будет его квадратным корнем. Выходит, что есть соответствие один-к-одному у квадратов натуральных чисел и понятия бесконечности. Это подтверждает идею, что подмножество бесконечных чисел может быть настолько же большим, как и набор бесконечных чисел, из которых вытекает это подмножество. Хотя может показаться, что это не так.
Проблема спящей красавицы

Спящая красавица ложится спать в воскресенье и монета подбрасывается. Если выпадает «решка», принцесса просыпается в понедельник, дает интервью и снова ложится спать, принимая снотворное. Если монетка падает на «орла», принцесса просыпается в понедельник и вторник, каждый раз дает интервью и снова ложится спать. Независимо от результата, она просыпается в среду и эксперимент завершается.
Парадокс возникает, когда вы пытаетесь выяснить, как она должна ответить на вопрос: «Как думаешь, как упала монетка?». Даже если учесть, что вероятность определения монетки 1/2, далеко не ясно, что спящая красавица должна сказать на самом деле. Некоторые утверждают, что фактическая вероятность 1/3, поскольку она не знает, какой был день, когда она проснулась. Есть три возможности: решка в понедельник, орел в понедельник и орел во вторник. Получается, ей нужно сказать «орел».
Источник
Комментариев нет:
Отправить комментарий